Momento de un fuerza con respeto a un eje !!!

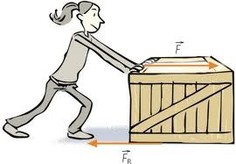
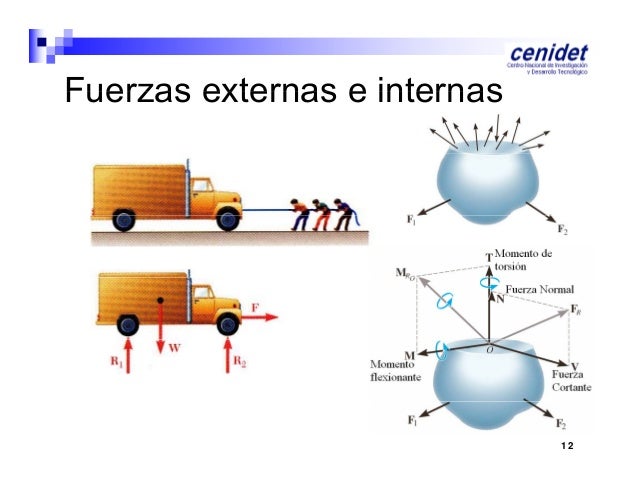
VEAMOS SOBRE MOMENTO ....

        Considere una fuerza F que actúa sobre un cuerpo rígido . Como se sabe, la fuerza F está representada por un vector que define la magnitud y su dirección. Sin embargo, el efecto de la fuerza sobre el cuerpo rígido también depende de su punto de aplicación A. La posición de A puede definirse de manera conveniente por medio del vector r que une al punto de referencia fijo O con A; a este vector se le conoce como el vector de posición de A.* El vector de posición r y la fuerza F definen el plano mostrado en la figura. El momento de F con respecto a O se define como el producto vectorial de r y F:

M0 = r x F 

                        De acuerdo con la definición del producto vectorial , el momento M0 debe ser perpendicular al plano que contiene el punto O y a la fuerza F. El sentido de M0 está definido por el sentido de la rotación que haría al vector r colineal con el vector F; un observador localizado en el extremo de M0 ve a esta rotación como una rotación en sentido contrario al movimiento de las manecillas del reloj. Otra forma de definir el sentido de M0 se logra por medio de la regla de la mano derecha: cierre su mano derecha y manténgala de manera que sus dedos estén doblados en el mismo sentido de la rotación que F le impartiría al cuerpo rígido alrededor de un eje fijo dirigido a lo largo de la línea de acción de M0 ; su dedo pulgar indicará el sentido del momento M0. Por último, representado con 6 el ángulo entre las líneas de acción del vector de posición r y la fuerza F, se encuentra que la magnitud del momento de F con respecto a O está dada por


M0 = rF sen o = Fd

                donde d representa la distancia perpendicular desde O hasta la línea de acción de F. En virtud de que la tendencia de la fuerza F a hacer girar al cuerpo rígido alrededor de un eje fijo perpendicular a la fuerza depende tanto de la distancia de F a dicho eje como de la magnitud de F, se observa que la magnitud de M0 mide la tendencia de la fuerza F a hacer rotar al cuerpo rígido alrededor de un eje fijo dirigido a lo largo de M0 . En el sistema de unidades del SI, donde la fuerza se expresa en newtons (N) y la distancia se expresa en metros (m), el momento de una fuerza estará expresado en newtons-metro (N • m). En el sistema de unidades de uso común en Estados Unidos, donde la fuerza se expresa en libras y la distancia en pies o en pulgadas, el momento de una fuerza se expresa en lb . ft o en lb . in. Se puede observar que a pesar de que el momento M0 de una fuerza con respecto a un punto depende de la magnitud, la línea de acción y el sentido de la fuerza, dicho momento no depende de la posición que tiene el punto de aplicación de la fuerza a lo largo de su lí­ nea de acción. En consecuencia, el momento M0 de una fuerza F no caracteriza a la posición del punto de aplicación de F.





RECORDEMOS QUE .....

si el momento va en sentido horario entonces su signo sera (-) negativo.
si el momento va en sentido antihorario su signo es (+) positivo.

Teorema de Varingnon

APRENDAMOS SOBRE ESTE TEOREMA ......

La propiedad distributiva de los productos vectoriales se puede emplear para determinar el momento de la resultante de varias fuerzas concurrentes. Si las fuerzas F j, F 2>. . . se aplican en el mismo punto A y si se representa por r al vector de posición A, a partir de la ecuación , se puede concluir que 

r x (F j + F 2 + ...) = r x F1 + r x F 2 + ...

Esto es, el momento con respecto a un punto dado O dé la resultante de varias fuerzas concurrentes es igual a la suma de los momentos de las distintas fuerzas con respecto al mismo punto O. Esta propiedad la descubrió el matemático francés Pierre Varignon (1654-1722) mucho antes de inventarse el álgebra vectorial, por lo que se le conoce como el teorema de Varignon. La relación  permite reemplazar el cálculo directo del momento de una fuerza F por el cálculo de los momentos de dos o más fuerzas componentes. Como se verá en la siguiente sección, por lo general la fuerza F será separada en sus componentes paralelas a los ejes coordenados. Sin embargo, será mucho más rápido en algunos casos descomponer a F en componentes no paralelas a los ejes coordenados 

Para utilizar estos teoremas debemos manejar:

• vectores
• producto vectorial
• descomponer las componentes rectangulares de un vector
• producto cruz
• vectores unitarios 

te dejamos un video donde explica detalladamente este teorema + ejemplos .....

Principio de transmisibilidad

ESTE PRINCIPIO ESTABLECE QUE .....

         establece que las condiciones de equilibrio o de movimiento de un cuerpo rígido permanecerán inalteradas si una fuerza F que actúa en un punto dado de ese cuerpo se reemplaza por una fuerza F ' que tiene la misma magnitud y dirección, pero que actúa en un punto distinto, siempre y cuando las dos fuerzas tengan la misma linea de acción . Las dos fuerzas, F v F ', tienen el mismo efecto sobre el cuerpo rígido y se dice que son equivalentes. Este principio establece que la acción de una fuerza puede ser transmitida a lo largo de su línea de acción, lo cual está basado en la evidencia experimental; no puede ser derivado a partir de las propiedades establecidas hasta ahora en este libro y, por tanto, debe ser aceptado como una ley experimental.

En el siguiente video podremos observar una mejor explicación de este tema.....

https://www.youtube.com/watch?v=zF19V4nfI8w

Fuerzas externas- internas

• FUERZAS EXTERNAS: 

           Las fuerzas externas representan la acción que ejercen otros cuerpos sobre el cuerpo rígido en consideración. Ellas son las responsables del comportamiento externo del cuerpo rígido. Las fuerzas externas causan que el cuerpo se mueva o aseguran que éste permanezca en reposo.

• FUERZAS INTERNAS:

              Las fuerzas internas son aquellas que mantienen unidas las partículas que conforman al cuerpo rígido. Si éste está constituido en su estructura por varias partes, las fuerzas que mantienen unidas a dichas partes también se definen como fuerzas internas. 

Empecemos a conocer el tema

¿ QUE ES CUERPO RÍGIDO?

             Al definir que un cuerpo rígido es aquel que no se defina, se supone que la mayoría de los cuerpos considerados en la mecánica elemental son rígidos. Sin embargo, las estructuras y máquinas reales nunca son absolutamente rígidas y se deforman bajo la acción de las cargas que actúan sobre ellas. A pesar de ello, por lo general esas deformaciones son peque­ñas y no afectan las condiciones de equilibrio o de movimiento de la estructura en consideración. No obstante, tales deformaciones son importantes en lo concerniente a la resistencia a la falla de las estructuras y están consideradas en el estudio de la mecánica de materiales.